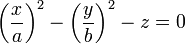30 décembre 2007
Le paraboloïde hyperbolique
En mathématiques,un paraboloïde est une surface du second degré de l'espace euclidien. Il fait donc partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie.
Certaines sections d'un paraboloïde avec un plan sont des paraboles. D'autres sont, selon le cas, des ellipses ou des hyperboles. On distingue donc les paraboloïdes elliptiques et les paraboloïdes hyperboliques.
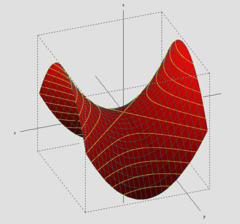
La photo et le schéma nous montrent le paraboloïde hyperbolique.Dans un repère bien choisi, son équation est de la forme
La forme particulière de cette surface lui vaut le surnom de selle de cheval. On reconnaît,sur le schéma, en jaune, des hyperboles " horizontales " et en violacé, des paraboles "verticales "
Libellés : Courbes ou surfaces mathématiques, Images mathématiques