Le Blog d'ABC Maths

1924 : Le physicien Wolfgang Pauli introduit la notion mathématique de spin.

2006: Inauguration du centre de recherche Neurospin dont le but est de "dévoiler " le cerveau.

Le centre de recherche inauguré hier par Dominique de Villepin disposera d'appareils d'imagerie par résonance magnétique nucléaire d'une puissance inégalée.

Définition simplifiée du spin:

La notion de spin permet de classer mathématiquement la façon dont se transforment les objets sous l'effet des rotations de l'espace à trois dimensions. De façon générale, un objet possède un spin s'il est invariant sous une rotation d'angle 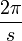. Par exemple

• Un objet sans symétrie particulière, par exemple une carte à jouer représentant un trois de trèfle, possède un spin 1 car il est nécessaire d'effectuer une rotation de pour qu'il se retrouve dans sa position de départ.
• Un objet possédant un peu plus de symétrie, comme une dame de pique par exemple, possède un spin deux car pour qu'elle revienne à sa position de départ, on peut se contenter de lui faire effectuer une rotation de .
• Une étoile à cinq branches possède un spin 5 car il est suffisant de lui faire faire une rotation de .

Libellés : Infos et actualités

Vénus est, après le Soleil et la Lune, l'astre le plus lumineux de notre ciel. Vue de la Terre, Vénus ne s'écarte que de 48° au maximum du Soleil, et est donc visible tantôt le matin, tantôt le soir. Appelée également "L'Etoile du Berger", elle est la première "étoile" qui s'allume au coucher du Soleil, et la dernière qui s'éteint dans les lueurs du matin. Connue dès l'Antiquité, les Egyptiens ainsi que les Grecs et les Romains ont longtemps cru qu'il s'agissait de deux planètes distinctes.

Vénus gravite en 224,7 jours sur une orbite quasi circulaire à une distance moyenne du Soleil de 108,2 millions de kilomètres. La rotation de la planète est extrêmement lente (242,98 jours, Terre=23h 56m 04s) et s'effectue dans le sens rétrograde. En raison d'une très faible inclinaison (2°) de l'axe de rotation par rapport au plan orbital, et d'une orbite quasi circulaire, les variations de saisons ne sont pas très importantes.

Sous bien des aspects, Vénus semble être la jumelle de la Terre. Elle a sensiblement le même diamètre (12.104 km, Terre= 12.756,34 km) et une masse un peu plus faible (0,817 masse terrestre). La densité de Vénus (5,1 g/cm³), assez proche de celle de la Terre (5,51 g/cm³), laisse penser qu'elle est constituée plus ou moins des mêmes matériaux.

La grande différence est causée par l'épaisseur de l'atmosphère, environ 90 fois plus dense que celle de la Terre et composée de 96,5% de dioxyde de carbone, qui concentre l’énergie solaire, provoquant un effet de serre pouvant être à l’origine de l’évaporation complète d'anciens océans vénusiens. Au lieu d'être juste un peu plus chaude que la Terre, la température au sol de Vénus est d'environ 500°C.

Libellés : Connaissance des planètes

Si on ne parvient pas à la solution d'un exercice au premier essai ,
il faut faire un deuxième essai , puis un troisième ...

Libellés : Récréation

"le simple battement d'ailes d'un papillon au Brésil pourrait déclencher une tornade au Texas". Cette métaphore, devenue emblématique du phénomène de sensibilité aux conditions initiales, est souvent interprétée à tort de façon causale : ce serait le battement d'aile du papillon qui déclencherait la tempète. Il n'en est rien. Cependant une donnée infime, imperceptible, peut aboutir à une situation totalement différente de celle calculée sans tenir compte de cette donnée infime.

Libellés : Histoire des mathématiques

e mathématicien Gustave Choquet, spécialiste de la théorie du potentiel, est mort, mardi 14 novembre. Il était âgé de 91 ans.

Libellés : Infos et actualités

Libellés : Histoire des mathématiques

Comment travailler plus efficacement

Eric Matrullo & Eric Maurette (Nathan)

192 pages, 16x24 cm
ISBN : 2-910350-00-2
Prix TTC : 12 €

Une synthèse de plus d'une centaine d'interviews de personnalités des mondes économique, politique, enseignant ou étudiant qui ont tous eu un parcours particulièrement brillant
"Comment travailler plus efficacement" est un ouvrage utile pour tous les lycéens et étudiants demandeurs de conseils pour améliorer leurs méthodes de travail.
Lire en particulier les pages décrivant la méthode consistant à faire fonctionner sa mémoire "en boucle" jusqu'à atteindre l'objectif souhaité, que les auteurs appellent "Feed-back".

Libellés : Infos et actualités, Infos et actualités ; en librairie

clique sur l'image pour l'agrandir

Libellés : Art et mathématiques, Images mathématiques

Le chou romanesco est une variété de chou fleur originaire d'Italie et plus précisément de Rome. Il est appelé aussi « brocoli à pomme ».

La disposition des bourgeons floraux en spirales régulières illustre les lois de la phyllotaxie. Un examen attentif montre que le nombre de spirales orientées dans le sens des aiguilles d'une montre et le nombre de spirales orientées en sens inverse sont deux nombres de la suite de Fibonacci, le rapport de ces nombres est une valeur approchée du nombre d'or. De plus sa géométrie autosimilaire fait qu'il est souvent cité comme un exemple de fractale naturel.

Libellés : Art et mathématiques, Images mathématiques

Caractéristiques Physiques
Diamètre	3 476 km
Diamètre apparent minimal	29' 23,2"
Diamètre apparent maximal	33' 28,8"
Masse	73.52*1021
Densité moyenne (Eau = 1)	3.341 g/cm³
Albédo géométrique	0.12
Pesanteur à l'équateur	1.627 m/s
Magnitude visuelle	-12,55
Température à la surface :
Régions exposées au Soleil	+ 117 °C
Régions non exposées	- 50 °C
Face non éclairée	- 163 °C
Atmosphère	très ténue

Libellés : Connaissance des planètes

IFS signifie Iterated Function Systems,
c'est à dire systèmes de fonctions itérées.
C'est une méthode pratique de réalisation d'images
fractales,qui permet également la compression d'images
quelconques.

Libellés : Art et mathématiques, Images mathématiques

Mars - Caractéristiques Physiques
Diamètre équatorial	6 804,9 km
Diamètre polaire	6 754,8 km
Aplatissement	0,007 36
Masse	6,4185×1023 kg
Masse (Terre = 1)	0.108
Masse volumique moyenne	3,934×103 kg/m³
Gravité à la surface	3,69 m/s²
Période de rotation sidérale	1,025 957 j soit 24,622 962 heures
Inclinaison de l'équateur sur l'orbite	25,19°
Albedo	0,15
Vitesse de libération	5,027 km/s
Température au sol	-25 °C
Pression atmosphérique	0,7-0,9 kPa
Atmosphère	-Dioxyde de carbone : 95,32 % -Diazote : 2,7 % -Argon : 1,6 % -Dioxygène : 0,13 % -Monoxyde de carbone : 0,07 % -Vapeur d'eau : 0,03 % -Traces de : Néon Krypton Xénon Ozone Méthane
Nbre de Satellites connus	2

Libellés : Connaissance des planètes

1° S et 1°GC : Un DS est prévu jeudi 16 novembre ( thème principal : Barycentre)
TGC : Un DS est prévu lundi 20 novembre (Etude de fonctions)

Libellés : Messages aux classes de G.Marion

Wendelin Werner , médaille Fields 2006 expose brièvement et à destination du grand public, ses sujets de recherche . (durée de la conférence : 50 mn)

Libellés : Conférence

La bouteille de Klein est une surface fermée, sans bord et non orientable, c'est-à-dire une surface pour laquelle on ne peut pas définir un « intérieur » et un « extérieur ». La bouteille de Klein a été décrite pour la première fois en 1882 par le mathématicien allemand Felix Klein. Elle est étroitement liée au ruban de Möbius .

Libellés : Courbes ou surfaces mathématiques

(Cliquer sur l'image)

Libellés : Courbes ou surfaces mathématiques, Images mathématiques

Les trajectoires des particules d'agrégats fractals bidimensionnels obtenus par collage de 50% de celles-ci lors de leurs collisions, dans un champ de gravitation vertical.

Une boite rectangulaire (bidimensionnelle) verticale est immergée dans un champ de gravitation. A l'intérieur de celle-ci, il y a 24*34=816 particules massives. Au départ, elles remplissent uniformément la boite ; leurs vitesses sont aléatoires en direction et constantes en module. Au cours du temps, elles interagissent avec le champ de gravitation qui les attire vers le bas et par des chocs avec les parois ainsi qu'entre-elles. Dans ce dernier cas, la moitie des particules (choisies initialement au hasard) peuvent se coller les unes aux autres (elles apparaissent en blanc), alors que les autres rebondissent (elles sont coloriées en fonction de leurs positions initiales). Progressivement les particules collantes (blanches) forment un agrégat fractal au-dessus de la paroi inférieure de la boite. Les autres particules (colorées) sont soit libres a l'intérieur de la boite, soit piégées par l'agrégat. Enfin, les courbes montrent les trajectoires de chacune des particules depuis l'instant initial.

Libellés : Courbes ou surfaces mathématiques

Les Shadoks - Cours de logique

I) Les passoires

On appelle passoire tout instrument sur lequel on peut définir trois sous-ensembles: l'intérieur, l'extérieur et les trous.

L'intérieur est généralement placé au dessus de l'extérieur et se compose le plus souvent de nouilles et d'eau. Les trous ne sont pas importants. En effet, une expérience simple permet de se rendre compte que l'on ne change pas notablement les qualités de l'instrument en réduisant de moitié le nombre de trous, puis en réduisant de moitié cette moitié... Etc... Etc... Et à la limite jusqu'a ce qu'il n'y ait plus de trous du tout.

D'où théorème: la notion de passoire est indépendante de la notion de trou et réciproquement.

On appelle passoires du premier ordre les passoires qui ne laissent passer NI les nouilles NI l'eau.

On appelle passoires du second ordre les passoires qui laissent passer ET les nouilles ET l'eau.

On appelle passoires du troisième ordre, ou passoires complexes, les passoires qui laissent passer quelquefois l'un ou l'autre et quelquefois pas. Pour qu'une passoire complexe laisse passer l'eau et pas les nouilles, il faut et il suffit que le diamètre des trous soit notablement inférieur au diamètre des nouilles.

Pour qu'une passoire complexe laisse passer les nouilles et pas l'eau, il faut et il suffit que le diamètre des trous soit notablement inférieur au diamètre de l'eau. Quand aux passoires du premier ordre qui ne laissent passer ni les nouilles ni l'eau, il y en a de deux sortes. Les passoires qui ne laissent passer ni les nouilles ni l'eau dans un sens ni dans l'autre

et celles qui ne laissent passer ni les nouilles ni l'eau que dans un sens seulement.

Ces passoires là, on les appelle des casseroles. Il y a trois sortes de casseroles. Les casseroles avec la queue à droite, les casseroles avec la queue à gauche et les casseroles avec pas de queue du tout. Mais celles-là on les appelle des autobus.

Il y a trois sorte d'autobus: les autobus qui marchent à droite; les autobus qui marchent à gauche et les autobus qui ne marchent ni d'un côté ni de l'autre. Mais ceux-là, on les appelle des casseroles. Il y a trois sortes de casseroles: les casseroles...

Libellés : Récréation

Libellés : Courbes ou surfaces mathématiques

1 x 8 + 1 = 9
12 x 8 + 2 = 98
123 x 8 + 3 = 987
1234 x 8 + 4 = 9876
12345 x 8 + 5 = 98765
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543
12345678 x 8 + 8 = 98765432
123456789 x 8 + 9 = 987654321

1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111

9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888

1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111=123456789 87654321

Libellés : Récréation

Quand on demande aux élèves des classes scientifiques de calculer approximativement la position du centre d'inertie du système terre-lune , sans leur fournir davantage de données , on constate que peu d'entre eux connaissent l'ordre de grandeur de la distance terre-lune ainsi que du rapport : (masse de la terre)/(masse de la lune)

Pour commencer la série "Connaissance des planètes"
voici les caractéristiques physiques de notre planète

Terre - Caractéristiques Physiques
Diamètre équatorial	12 756,28 km
Diamètre polaire	12 713,55 km
Aplatissement aux pôles	0,003 352 9 1÷298,242
Masse	5,973 6×1024 kg
Masse volumique moyenne	5,515×103 kg/m³
Gravité moyenne à la surface	9,780 m/s²
Période de rotation sidérale	0,997 258 jours soit 23,934 19 heures
Inclinaison de l'équateur sur l'orbite	23,45°
Albedo	0,367
Vitesse de libération	11,186 km/s
Température moyenne au sol	12 °C
Pression atmosphérique	101 325 Pa
Atmosphère	-Azote N2 : 78,11 % -Oxygène O2 : 20,953 % -Argon Ar : 0,934 % -Eau H2O (vapeur) : de 0 à 7 % -Dioxyde de carbone CO2 : de 0,01 à 0,1 %
Nbre de Satellites connus	1

Libellés : Connaissance des planètes

Complexités. Aux limites des mathématiques et de l'informatique.
de Jean-Paul Delahaye
Éditeur : BELIN - Pour La Science
Collection : Bibliothèque scientifique
(15 octobre 2006)

On doit aux mathématiques et à l’informatique la maîtrise des complexités rencontrées dans toutes les sciences, car elles fabriquent les outils pour les penser et en créer de nouvelles, à notre service : les ordinateurs sont les objets artificiels les plus complexes jamais créés par l’homme. Cependant mathématiques et informatique flirtent avec les limites de l’intelligence. Quelle est la mémoire totale de l’humanité actuelle et comment évolue-t-elle ? Quels sont les plus grands calculs envisageables avec notre technologie ? Qu’est-ce qu’un très grand nombre, et comment le noter ? L’intelligence humaine est-elle rattrapée par celle des machines ? Les objets mathématiques existent-ils vraiment ? La simulation informatique nous plonge-t-elle dans un monde d’illusions ? Quelles sont les caractéristiques de l’ordinateur ultime, et l’univers entier est-il lui-même un immense ordinateur ? Cet ouvrage est fondé sur l’actualité scientifique et les spéculations théoriques qu’elle suscite ces dernières années en mathématiques et en informatique. Il invite à partager le troublant vertige que les chercheurs ressentent en construisant notre avenir. En partenariat avec le magazine Pour La Science.

Libellés : Infos et actualités

Sources: Institut des Hautes Études Scientifiques et www.techno-science.net
* 1975 - Prix Aimé-Berthé de l'Académie des sciences
* 1976 - Prix Peccot-Vimont du Collège de France
* 1977 - Médaille d'argent du CNRS
* 1980 - Prix Ampère de l'Académie des sciences
* 1982 - Médaille Fields, pour ses travaux sur les algèbres d'opérateurs
* 2000 - Prix Clay
* 2001 - Prix Crafoord
* 2004 - Médaille d'or du CNRS

Libellés : Conférence

Exclusivement réservé aux petites sections de maternelle

Libellés : Récréation

Superbe réponse de Gilbert Walusinski aux remises en cause des mathématiques et de leur enseignement qu'on lit de façon récurrente dans la presse d'aujourd'hui.

Libellés : Infos et actualités

En vidant les programmes, en abaissant les exigences, en déstructurant les enseignements, les réformes successives ont conduit à un renforcement sans précédent de la sélection par la naissance et par l'argent : les familles défavorisées ou non francophones sont terriblement pénalisées lorsque ce que l’on n’apprend plus à l’Ecole doit s’apprendre à la maison, ou dans des cours de soutien payants.

Laisserons-nous l’Ecole abandonner sa mission d’instruction, et des services payants se substituer à elle ?
Voulons-nous mettre fin à la promotion sociale par l’Ecole ?
Accepterons-nous d'entrer dans un nouvel obscurantisme ?
Nous le refusons de toutes nos forces.

Notre cause est trans-partisane : alter-mondialistes, libéraux, communistes, gaullistes, socialistes ou chrétiens-démocrates, croyants, agnostiques ou libres penseurs, enseignants et parents d'élèves, nous sommes rassemblés par un même attachement à l'Ecole et une même volonté : refonder l’instruction publique sur la transmission de savoirs riches, solides et cohérents, et sur la liberté pédagogique des professeurs.

Libellés : Infos et actualités