24 décembre 2011

 

Enigme de Noël .

Le père Noël a un nombre impair de cadeaux divers à distribuer. 
S'il choisit n'importe lequel de ces cadeaux, alors il peut toujours s'arranger pour répartir les cadeaux restants en 2 lots comportant chacun le même nombre de  cadeaux, les deux lots étant de même prix.
Tous les cadeaux valent-ils le même prix ?
Bon Noël équitable .

Libellés :


# abcmaths @ 08:21

22 décembre 2011

 

Maïeutique.

Étant donné un carré, construire un carré d'aire double. Voici comment, selon Platon, Socrate l'aurait proposé à un esclave (dialogue Le Ménon) afin de démontrer que la science est en chacun de nous :
Socrate veut amener le jeune esclave à trouver la marche à suivre pour construire un carré dont la surface serait le double de l'original (en gras sur la figure). Le côté du carré vaut 2. Il a donc une surface de 4, et il faut construire un carré dont l'aire vaut 8. 
Comment ? L'esclave répond qu'il faut doubler la longueur des côtés. L'erreur du garçon semble être la première étape, ou le préliminaire, de la réminiscence .
Socrate trace le carré que lui propose l'esclave : il faut se rendre à l’évidence, il est non deux, mais quatre fois plus grand que l'original.
Le jeune garçon propose alors de construire un carré dont le côté vaut 3. Or ce carré a une aire de 9, ce qui n'est pas ce que l'on cherche.
L'esclave est désormais dans l'embarras.[...] mais il est clair, affirme Socrate, que le garçon a fait beaucoup de chemin : « [...] à présent le voilà qui considère désormais qu'il est dans l’embarras, et tandis qu'il ne sait pas, au moins ne croit-il pas non plus qu'il sait » . Il est maintenant dans une meilleure situation qu'avant.
 En particulier, cela est profitable parce que jamais on ne cherche ce qu'on croit savoir.
Socrate trace les diagonales. Il apparaît que le carré construit sur la diagonale du carré initial est le carré recherché. L'esclave le découvre et affirme maintenant que c'est sur cette ligne que l'on construit un carré deux fois plus grand que le premier. Mais il l'ignorait complètement il y a un instant. Il faut en conclure : 
« Chez l'homme qui ne sait pas, il y a donc des opinions vraies au sujet de choses qu'il ignore »  
                 
Ce principe philosophique initié par Socrate porte le nom de maïeutique, du grec maieutiké : art d'accoucher, méthode reposant sur l'interrogation et se proposant d'amener un interlocuteur à prendre conscience de ce qu'il sait implicitement .


Source

Libellés : ,


# abcmaths @ 07:05

20 décembre 2011

 

Espérance mathématique et foi chrétienne .



Notes :
1) L'espérance mathématique d'une variable aléatoire est l'équivalent en probabilité de la moyenne d'une série statistique en statistiques. Elle se note E(X) et se lit espérance de X. C'est une valeur numérique permettant d'évaluer le résultat moyen (attendu ou "espéré") d'une expérience aléatoire. Elle permet par exemple de mesurer le degré d'équité d'un jeu de hasard; elle est alors égale à la somme des gains (et des pertes) pondérés par la probabilité du gain (ou de la perte). Lorsque l'espérance est égale à 0, le jeu est dit équitable, les chances de gagner étant égales à celles de perdre .
2) Le pari de Pascal :
« Vous avez deux choses à perdre : le vrai et le bien, et deux choses à engager : votre raison et votre volonté, votre connaissance et votre béatitude; et votre nature a deux choses à fuir : l'erreur et la misère. Votre raison n'est pas plus blessée, en choisissant l'un que l'autre, puisqu'il faut nécessairement choisir. Voilà un point vidé. Mais votre béatitude ? Pesons le gain et la perte, en prenant croix que Dieu est. Estimons ces deux cas : si vous gagnez, vous gagnez tout ; si vous perdez, vous ne perdez rien. Gagez donc qu'il est, sans hésiter. »
Esperamos, donc !
Et bonnes fêtes de Noël !

Libellés :


# abcmaths @ 17:46

16 décembre 2011

 

En direct de Kourou.

Pour son deuxième lancement Soyuz depuis le Centre Spatial Guyanais, Arianespace mettra en orbite le satellite Pléiades 1 du CNES, les 4 satellites du Démonstrateur ELISA de la DGA et le satellite d’observation de la Terre, SSOT pour les Forces Armées chiliennes. 


Samedi 17 à 03: 03:48  (Heure de Paris)

Libellés :


# abcmaths @ 12:11

15 décembre 2011

 

La formule Villani .

Le temps des vacances de Noël, France Info a fait appel à Cedric Villani .
Cédric Villani, médaille Fields en 2010, le « Nobel des maths », propose un rendez-vous quotidien sur France Info aux côtés de Sandrine Marcy du lundi 19 au vendredi 30 décembre, à 5h45, 9h40, 13h50, 18h40 et 21h55.
Chaque jour, il nous  expliquera en quoi les mathématiques touchent notre quotidien en abordant des thèmes variés comme, la météorologie, l'économie ou encore les transports.


Cédric Villani, éminent mathématicien et vulgarisateur hors pair, médaille Fields 2010, professeur de l'Université de Lyon - est directeur de l'Institut Henri Poincaré (CNRS / UPMC).

Libellés :


# abcmaths @ 12:12

13 décembre 2011

 

La revanche de Pythagore - Arturo Sangalli .

Pythagore de Samos n'a laissé aucun écrit. Du moins le croyait-on jusqu'à ce qu'un jeune mathématicien américain, Jules Davidson, et un historien anglais, Elmer Galway, découvrent les étranges agissements d'une secte de néo-pythagoriciens et partent à la recherche d'un mystérieux document qui pourrait résoudre quelques-unes des énigmes les plus actuelles des mathématiques...


Biographie de l'auteur:
Arturo Sangalli - Docteur en mathématiques, ancien enseignant chercheur, journaliste scientifique, traducteur et auteur d'ouvrages de vulgarisation .

Libellés :


# abcmaths @ 10:03

12 décembre 2011

 

Pour cent âge éducatif .

Dans mon petit lycée, qui compte 50 professeurs, n'enseignent que des jeunes et des vieux.
Mais 20 % des jeunes professeurs se prennent pour des vieux et 10 % des vieux se prennent pour des jeunes.
Les autres se prennent pour ce qu’ils sont.
A tous les professeurs de ce drôle de lycée, on pose la même question :
“Êtes-vous vieux ?”
34 % des professeurs répondent oui .

Alors, combien de jeunes professeurs dans mon lycée ?

Libellés :


# abcmaths @ 07:31

11 décembre 2011

 

L/l = (L+l)/L



Le nombre d'or est la proportion, définie initialement en géométrie, comme l'unique rapport entre deux longueurs telles que le rapport de la somme des deux longueurs (L+l) sur la plus grande (L) soit égal à celui de la plus grande (L) sur la plus petite (l), 
c'est-à-dire lorsque (L+l)/l = L/l. 
Le nombre d'or est maintenant souvent désigné par la lettre φ (phi).
Pour en savoir plus

Musique de la vidéo: "Concerto pour Elle" de Saint-Preux.

Libellés :


# abcmaths @ 11:28

06 décembre 2011

 

Googler des graphiques .

Google permet maintenant de tracer des représentation graphiques de fonctions, en renseignant l’expression de la fonction dans la barre de recherche,
comme sur cet exemple


Pas de courbes paramétrées encore, mais cela va sans doute venir

Allez, jouez!  Si le coeur vous en dit 

Libellés : ,


# abcmaths @ 17:10

05 décembre 2011

 

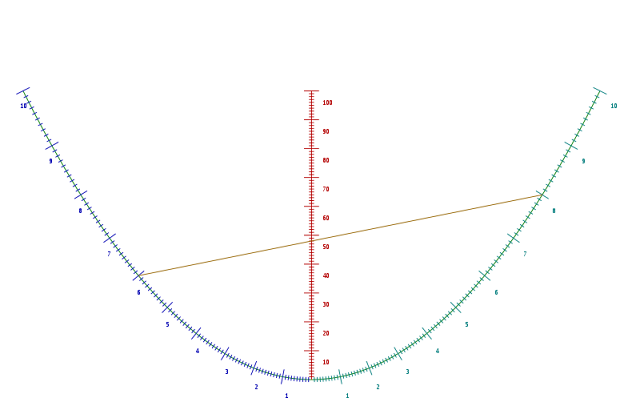
Enigme pour les élèves de première : Multiplicateur de Möbius .

Pour effectuer le produit de 6 par 8 (par exemple), il suffit de tirer un trait  entre la graduation 6 de la branche bleue et la graduation 8 de la branche verte. 
Ci-dessus, on voit que le trait tracé coupe l'axe rouge sur la graduation 48 .

Libellés :


# abcmaths @ 06:57

03 décembre 2011

 

Mathématiques, un dépaysement soudain - Aperçu de l'exposition .




Plus d'infos ici

Libellés : ,


# abcmaths @ 16:23

This page is powered by Blogger. Isn't yours?