16 octobre 2015
Sans trucage .
02 mai 2015
Le problème de Freudenthal.
J'ai retrouvé l'énigme célèbre qui a probablement inspiré le problème dit singapourien qui a "fait le buzz" sur internet au mois d'avril dernier .
Problème de Freudenthal :
On choisit deux entiers X et Y, avec 1 < X < Y et X + Y ≤ 100.
On indique à Patricia le produit P de X et Y.
On indique à Sylvie la somme S de X et Y.
Le dialogue est alors le suivant :
Patricia : « Je ne sais pas quels sont les nombres X et Y. »
Sylvie : « Je savais que vous ne connaissiez pas X et Y. »
Patricia : « Eh bien alors, maintenant, je connais X et Y. »
Sylvie : « Eh bien, moi aussi je les connais maintenant. »
Trouvez X et Y.
Ce problème parut pour la première fois en néerlandais en 1969 dans la revue Nieuw Archief voor Wiskunde
dont Freudenthal était rédacteur de la rubrique " problèmes " .
Hans Freudenthal (17 septembre 1905 – 13 octobre 1990) était un mathématicien allemand, naturalisé néerlandais, spécialiste en topologie algébrique, mais dont les contributions ont largement débordé ce domaine .
La solution se trouve sur la page Wikipédia de Freudenthal.
Un article intitulé " l'incroyable problème de Freudenthal" a été publié par Jean Paul Delahaye (Professeur d'informatique à l'Université des Sciences et Technologies de Lille) sur le site Interstices en 2008 .
Problème de Freudenthal :
On choisit deux entiers X et Y, avec 1 < X < Y et X + Y ≤ 100.
On indique à Patricia le produit P de X et Y.
On indique à Sylvie la somme S de X et Y.
Le dialogue est alors le suivant :
Patricia : « Je ne sais pas quels sont les nombres X et Y. »
Sylvie : « Je savais que vous ne connaissiez pas X et Y. »
Patricia : « Eh bien alors, maintenant, je connais X et Y. »
Sylvie : « Eh bien, moi aussi je les connais maintenant. »
Trouvez X et Y.
Ce problème parut pour la première fois en néerlandais en 1969 dans la revue Nieuw Archief voor Wiskunde
dont Freudenthal était rédacteur de la rubrique " problèmes " .
Hans Freudenthal (17 septembre 1905 – 13 octobre 1990) était un mathématicien allemand, naturalisé néerlandais, spécialiste en topologie algébrique, mais dont les contributions ont largement débordé ce domaine .
La solution se trouve sur la page Wikipédia de Freudenthal.
Un article intitulé " l'incroyable problème de Freudenthal" a été publié par Jean Paul Delahaye (Professeur d'informatique à l'Université des Sciences et Technologies de Lille) sur le site Interstices en 2008 .
Libellés : Enigme
# abcmaths @ 13:45
18 avril 2015
Vous avez dit problème singapourien ?
Nos fantastisques " journalistes" ont tous titré, comme ici, par exemple :
Réussirez-vous à résoudre ce problème de maths singapourien
ou là:
Le problème de maths venu de Singapour qui agace internet
(mais aussi sur le monde.fr, le point.fr, l'express.fr, etc...)
que le problème qui a fait le buzz sur la toile ces derniers jours, était une création de Singapour et leurs articles laissent croire que les élèves de Singapour seraient géniaux, comparé aux élèves occidentaux.
Voici ci dessous le même type de problème, posé sous une forme légèrement différente et nettement plus difficile, à mes élèves de terminale en 2007 :
C'est ici sur le blog
Klomac et Barriton jouent avec Toutrouge. Ils lui demandent de choisir deux nombres entre 2 et 100. Toutrouge tend un papier à Klomac en lui indiquant qu'il s'agit de la somme de ces deux nombres. Puis il tend un papier à Barriton avec le produit de ces deux nombres. Suit un discours étonnant:
B : Ce produit ne me permet pas de déterminer quels sont ces deux nombres.
K: Je le savais!
B: Alors je connais ces 2 nombres.
K: Dans ce cas, moi aussi!
Quels sont ces deux nombres ?
Pour comparer, voir mon post précédent, ici
Réussirez-vous à résoudre ce problème de maths singapourien
ou là:
Le problème de maths venu de Singapour qui agace internet
(mais aussi sur le monde.fr, le point.fr, l'express.fr, etc...)
que le problème qui a fait le buzz sur la toile ces derniers jours, était une création de Singapour et leurs articles laissent croire que les élèves de Singapour seraient géniaux, comparé aux élèves occidentaux.
Voici ci dessous le même type de problème, posé sous une forme légèrement différente et nettement plus difficile, à mes élèves de terminale en 2007 :
C'est ici sur le blog
Enigme pour les vacances (pour les élèves de terminale)
B : Ce produit ne me permet pas de déterminer quels sont ces deux nombres.
K: Je le savais!
B: Alors je connais ces 2 nombres.
K: Dans ce cas, moi aussi!
Quels sont ces deux nombres ?
Pour comparer, voir mon post précédent, ici
Libellés : Enigme, Infos et actualités
# abcmaths @ 10:53
14 avril 2015
Puissance de Facebook .
Je me souviens d'avoir posé ce problème de logique (ou une variante quasi-similaire) à mes élèves il y a au moins une bonne dizaine d'années . Quelques bons élèves avaient été intéressés et l'énigme avait été transmise à quelques frères ou soeurs mais le problème n'avait pas fait le tour du lycée .
Le 12 avril dernier, un présentateur de la chaîne télévisuelle Channel 8, à Singapour, poste sur sa page Facebook la photo du même problème de mathématiques.
Elle va finir par causer un débat mondial sur internet.
Albert et Bernard sont devenus amis avec Cheryl et ils veulent connaître le jour de son anniversaire. Cheryl leur a donné une liste de 10 dates possibles.
– le 15, 16 ou 19 mai – le 17 ou 18 juin – le 14 ou 16 juillet – le 14, 15 ou 17 août .
Cheryl communique séparément et respectivement à Albert et Bernard le mois et le jour de son anniversaire.
Albert dit : "Je ne sais pas quand est l’anniversaire de Cheryl, mais je sais que Bernard ne sait pas non plus."
Bernard : "Au début je ne savais pas quand est l’anniversaire de Cheryl, mais maintenant je sais."
Albert réplique : " Dans ce cas je sais aussi quand est son anniversaire. "
Quelle est la date de l’anniversaire de Cheryl ?
Le 12 avril dernier, un présentateur de la chaîne télévisuelle Channel 8, à Singapour, poste sur sa page Facebook la photo du même problème de mathématiques.
Elle va finir par causer un débat mondial sur internet.
Albert et Bernard sont devenus amis avec Cheryl et ils veulent connaître le jour de son anniversaire. Cheryl leur a donné une liste de 10 dates possibles.
– le 15, 16 ou 19 mai – le 17 ou 18 juin – le 14 ou 16 juillet – le 14, 15 ou 17 août .
Cheryl communique séparément et respectivement à Albert et Bernard le mois et le jour de son anniversaire.
Albert dit : "Je ne sais pas quand est l’anniversaire de Cheryl, mais je sais que Bernard ne sait pas non plus."
Bernard : "Au début je ne savais pas quand est l’anniversaire de Cheryl, mais maintenant je sais."
Albert réplique : " Dans ce cas je sais aussi quand est son anniversaire. "
Quelle est la date de l’anniversaire de Cheryl ?
Libellés : Enigme, Infos et actualités
# abcmaths @ 18:53
01 avril 2015
Géométrie d'avril .
Avec 5 allumettes (toutes de même longueur) on construit un poisson comme indiqué sur la figure. Que vaut l'angle x?
Libellés : Enigme, Récréation
# abcmaths @ 08:18
24 décembre 2011
Enigme de Noël .
Le père Noël a un nombre impair de cadeaux divers à distribuer.
S'il choisit n'importe lequel de ces cadeaux, alors il peut toujours s'arranger pour répartir les cadeaux restants en 2 lots comportant chacun le même nombre de cadeaux, les deux lots étant de même prix.
Tous les cadeaux valent-ils le même prix ?
Bon Noël équitable .
S'il choisit n'importe lequel de ces cadeaux, alors il peut toujours s'arranger pour répartir les cadeaux restants en 2 lots comportant chacun le même nombre de cadeaux, les deux lots étant de même prix.
Tous les cadeaux valent-ils le même prix ?
Bon Noël équitable .
Libellés : Enigme
# abcmaths @ 08:21
12 décembre 2011
Pour cent âge éducatif .
Dans mon petit lycée, qui compte 50 professeurs, n'enseignent que des jeunes et des vieux.
Mais 20 % des jeunes professeurs se prennent pour des vieux et 10 % des vieux se prennent pour des jeunes.
Les autres se prennent pour ce qu’ils sont.
A tous les professeurs de ce drôle de lycée, on pose la même question :
“Êtes-vous vieux ?”
34 % des professeurs répondent oui .
Alors, combien de jeunes professeurs dans mon lycée ?
Mais 20 % des jeunes professeurs se prennent pour des vieux et 10 % des vieux se prennent pour des jeunes.
Les autres se prennent pour ce qu’ils sont.
A tous les professeurs de ce drôle de lycée, on pose la même question :
“Êtes-vous vieux ?”
34 % des professeurs répondent oui .
Alors, combien de jeunes professeurs dans mon lycée ?
Libellés : Enigme
# abcmaths @ 07:31
05 décembre 2011
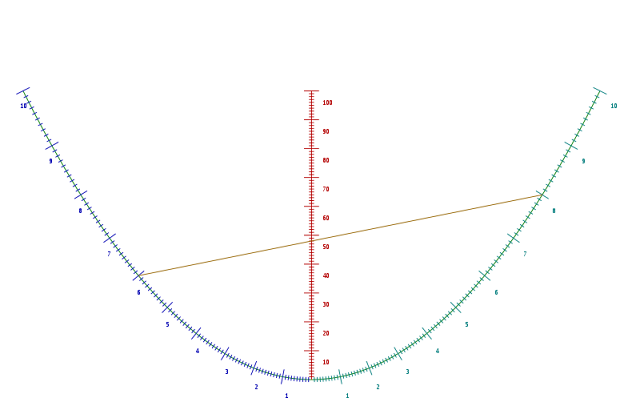
Enigme pour les élèves de première : Multiplicateur de Möbius .
Ci-dessus, on voit que le trait tracé coupe l'axe rouge sur la graduation 48 .
Libellés : Enigme
# abcmaths @ 06:57
28 novembre 2011
Pour les élèves de seconde.
Déterminer, sans calculatrice, le nombre :
(2011)^2 - (2010)*(2012)
Libellés : Enigme
# abcmaths @ 03:47
24 novembre 2011
le 2011° nombre .
On construit une suite de nombres.
2010 en est le premier.
Le deuxième est obtenu en faisant la somme des carrés des chiffres de 2010, à savoir :
2² + 0² + 1² + 0² ce qui donne 5.
On continue ainsi. Le troisième nombre est alors 25 et le quatrième 29 .
Quel sera le 2011 ° nombre ?
2010 en est le premier.
Le deuxième est obtenu en faisant la somme des carrés des chiffres de 2010, à savoir :
2² + 0² + 1² + 0² ce qui donne 5.
On continue ainsi. Le troisième nombre est alors 25 et le quatrième 29 .
Quel sera le 2011 ° nombre ?
Libellés : Enigme
# abcmaths @ 07:17
17 novembre 2011
Arithmétique en couleur .
On décide d’attribuer une couleur (rouge ou bleu) aux nombres entiers naturels en respectant les règles suivantes :
– Le nombre 0 est bleu.
– Si un nombre entier peut s’écrire comme la somme d’au moins deux entiers rouges distincts, alors il est bleu.
Dans le cas contraire, il est rouge.
Alors, quels entiers sont rouges ?
– Le nombre 0 est bleu.
– Si un nombre entier peut s’écrire comme la somme d’au moins deux entiers rouges distincts, alors il est bleu.
Dans le cas contraire, il est rouge.
Alors, quels entiers sont rouges ?
Libellés : Enigme
# abcmaths @ 08:18
19 octobre 2011
J moins 1 .
Troisième et dernier indice :
Altitude : 23 222 km
Altitude : 23 222 km
Libellés : Enigme, Messages aux classes de G.Marion
# abcmaths @ 12:34
18 octobre 2011
J moins 2 .
Deuxième indice :
Inclinaison : 54.7 degrés
Libellés : Enigme, Messages aux classes de G.Marion
# abcmaths @ 12:34
17 octobre 2011
J moins 3 .
Premier indice :
1 400 kg environ .
Note aux élèves :
Non, non, il ne s'agit pas du poids de ma voiture chargée à bloc lors du jour J de mon départ en vacances scolaires.
Non, non et non ce n'est pas la masse totale des joueurs de l'équipe de France de rugby et la finale n'est pas dans 3 jours !
1 400 kg environ .
Note aux élèves :
Non, non, il ne s'agit pas du poids de ma voiture chargée à bloc lors du jour J de mon départ en vacances scolaires.
Non, non et non ce n'est pas la masse totale des joueurs de l'équipe de France de rugby et la finale n'est pas dans 3 jours !
Libellés : Enigme, Messages aux classes de G.Marion
# abcmaths @ 12:34
13 août 2011
L'énigme européenne .
" La Suisse emprunte actuellement à un taux d’intérêt de 1,5 % , l’Allemagne au taux de 2,7 %, la France à 3,1% et le Royaume-Uni à 3,3 %
Mais quand le Portugal emprunte, c'est à 6,8% ; l’Irlande, elle, doit payer 9 % et la Grèce 12 %.(ces taux sont de la semaine dernière )...
...Un jour, peut-être, le gouvernement fédéral de l'Europe Unie émettra des emprunts d'état européens garantis par L'Europe, toute l'Europe, pour servir les peuples européens, tous les peuples. Ja, wir müssen es machen. Ja, wir können !
Esperamos ."
L'article complet est ici
" Créer des "Eurobonds".C'est ce que l'économiste Daniel Cohen (membre du conseil de surveillance du Monde) appelle "la bombe à neutrons". Elle consisterait à mettre tout ou partie de la dette des Etats de l'eurozone sans distinction de pays ... "
L'article complet est là.
Aujourd'hui , dans Le Figaro :" Les eurobonds auraient permis d'éviter d'arriver à la crise de la dette, a estimé samedi lors d'une conférence de presse à Rome le ministre italien de l'Economie Giulio Tremonti, qui a jugé "fondamentale une plus grande consolidation des finances publiques en Europe...
"S'il y avait eu les eurobonds, nous ne serions pas arrivés à (la crise d') aujourd'hui", a affirmé le ministre"
L'article est ici
Rappelons que :
L’Union européenne est la deuxième puissance économique mondiale (et même la première parfois suivant le taux de change euro/dollar) avec près de 30% du PIB mondial; elle est aussi la première puissance agricole, industrielle et de service au monde.
Mais encore :
la première puissance sportive de la planète,
la première puissance nucléaire civile,
la deuxième puissance spatiale du monde,
la deuxième puissance technique du monde,
la troisième puissance démographique du monde,
la troisième puissance nucléaire militaire.
La région la moins inégalitaire du monde .
Elle serait, en outre, dotée des meilleurs services secrets au monde .
L'Allemagne, à elle seule, avec 13 fois moins d'habitants que la Chine, était encore il y a quelque mois la première puissance exportatrice du monde (elle a été dépassée par la Chine depuis peu).
Et toute cette puissance serait incapable d'intervenir efficacement contre les effets, dévastateurs pour les peuples, de la spéculation boursière et se laisserait dicter sa loi par trois agences de notation dont la pertinence et la neutralité sont loin d'être au dessus de tout soupçon ?
Gageons que la crise va enfin faire naître l'Europe politique devenue indispensable.(1)
Sinon, pour le citoyen lambda qui à juste titre ne comprend pas, l'Europe sera, au pire une plaisanterie, au mieux une énigme (2) .
(1) Certaines nations sont moins pressées que d'autres, c'est vrai :
"J'exclus ces euro-obligations tant que les Etats membres mènent leur propre politique budgétaire", a déclaré aujourd'hui-même le ministre allemand des finances, M. Schäuble.
(2) Même les Chinois ne comprennent pas:
"Quand des dizaines de milliards de dollars s'évaporent en un jour mercredi sur les marchés américain et européens après des spéculations selon lesquelles la note du crédit de la France serait en danger et que le président français Nicolas Sarkozy rentrerait d'urgence pour mener une "guerre de défense du crédit", on ne peut s'empêcher de demander: qu'est-ce qui ne tourne pas rond en Occident? "
écrit récemment l'agence officielle Chine nouvelle .
PS:
Le 14/12/1965, lors d'un entretien avec Michel Droit, entre les deux tours de l'élection présidentielle, le général de Gaulle prononce sa célèbrissime "petite phrase" :"Bien entendu, on peut sauter sur sa chaise comme un cabri en disant l'Europe ! l'Europe ! l'Europe !... mais cela n'aboutit à rien et cela ne signifie rien"
Libellés : Enigme, Infos et actualités
# abcmaths @ 14:39
01 août 2011
2011 et les 1 : Enigme pour les collègiens ( et leurs parents)
Cette année compte déjà quatre dates remarquablement économes en chiffres :
1/1/11
11/1/11
1/11/11
11/11/11
Mieux:
Prenez le nombre constitué des deux derniers chiffres de votre année de naissance .
Ajoutez votre âge à ce nombre (plus exactement l'âge que vous avez/aurez cette année).
1/1/11
11/1/11
1/11/11
11/11/11
Mieux:
Prenez le nombre constitué des deux derniers chiffres de votre année de naissance .
Ajoutez votre âge à ce nombre (plus exactement l'âge que vous avez/aurez cette année).
Libellés : Enigme
# abcmaths @ 04:55
28 juillet 2011
Enigme de juillet 2011.
15 jours de "week-end" en un seul mois ! (16 si on ajoute le jeudi 14 juillet) . Un mois où les fins de de semaine sont plus denses que les semaines elles-mêmes . Diantre !
Il faudra attendre longtemps, très longtemps, (des siècles peut-être ?), pour qu'une telle distribution se reproduise .
Combien d'années exactement ?
Libellés : Enigme
# abcmaths @ 10:06
09 février 2011
2012 puissance X : Une question essentielle !
Combien l’équation 2010^x + 2011^x= 2012^x a-t-elle de racines réelles ?
Libellés : Enigme
# abcmaths @ 04:14
19 janvier 2011
A fond sur ma mob à basse consommation.
En une heure, à fond sur ma mob, j’ai parcouru la distance séparant deux bornes kilométriques portant la même paire de chiffres .
Trois heures plus tard, à la même vitesse constante, j’atteins une troisième borne indiquant la même paire de chiffres mais séparés par un 9 .
Après un certain temps, toujours à la même vitesse constante, je croise une quatrième borne portant les trois mêmes chiffres !
Une heure plus tard et à la même vitesse constante, une cinquième borne toujours avec les trois mêmes chiffres !
Alors, à quelle vitesse elle carbure, ma mob, et quelle est son autonomie ?
Libellés : Enigme
# abcmaths @ 04:35
14 janvier 2011
Qu' est-ce ?
