30 novembre 2007
Votre signature vaut plus que nous ne l'imaginez
Libellés : Infos et actualités
Quelques chiffres de la respiration de la planète Terre.
Visibilité sur le Web des instituts de recherche : Le CNRS est classé 6°.
Ce classement a été réalisé par Webometrics dépendant du «Laboratorio de Internet» (Espagne) qui étudie les données concernant la communication universitaire sur Internet.
Source ici
Ne cliquez pas ici, c'est encore de la pub!
Classement européen :
Libellés : Infos et actualités
Ordre de grandeur
En général, un ordre de grandeur est une fourchette de valeurs qui va de un dixième à dix fois la grandeur nominale (c'est-à-dire la grandeur énoncée). Ainsi, si l'on dit que
L’ordre de grandeur de la distance Terre-Lune est de 108 mètres car la distance Terre-Lune est de 384 000 km (100 000 kilomètres = 100 000 000 mètres =108 mètres).
L’ordre de grandeur du diamètre d’un cheveux est de 10-4 mètres car un cheveux possède un diamètre d’environ 80 microns et 100 microns = 0.0001 mètres = 10-4 mètre
Taille nanométrique : 10-9 m , 10-8 m, 10-7 m
Ordre de grandeur des plus petites espèces vivantes (de l'ordre de 1 nm à 1 µm, soit 10-9 à 10-6 m) :
- 10-8 m : les virus ont une taille allant de 20 à 450 nm
- 10-7 m : la longueur d'onde de la lumière visible s'étend de 380 à 740 nm
Taille micrométrique : 10-6 à 10-3 m
Ordre de grandeur des cellules (de l'ordre de 1 µm à 1 mm, soit 10-6 à 10-3 m) :
- 10-6 m : une bactérie mesure de 1 à 10 µm
- 10-4 m : un cheveu mesure à peu près 80 µm de diamètre
Taille humaine : 10-3 à 10³ m
Ordre de grandeur des longueurs courantes dans le domaine humain (de l'ordre de 1 mm à 1 km, soit 10-3 à 10³ m) :- 10-2 m = 1 cm :
- ordre de grandeur de la plupart des insectes sociaux : fourmis, abeilles, termites ;
- ordre de grandeur des composants électroniques.
- 100 m = 1 m :
- un volume de 1 000 L est contenu dans un cube de 1 m d'arête ;
- la taille humaine moyenne est d'environ 1,6 m pour une femme et 1,8 m pour un homme ;
- dans une habitation française typique, la hauteur de plafond des pièces est d'environ 2,5 m.
- 101 m = 10 m :
- sur certaines côtes, l'amplitude des marées peut atteindre 10 m ;
- lors du tsunami du 26 décembre 2004, certaines vagues ont atteint 15 m de hauteur.
- 10² m = 100 m :
- 100 m est la longueur du côté d'un stade ;
- 400 m est la circonférence d'un stade d'athlétisme ;
- le plus haut gratte-ciel (hors antenne), Taipei 101, fait 448 m de haut.
Taille planétaire : 10³ à 108 m
Ordre de grandeur des phénomènes géologiques (de l'ordre de 1 à 100 000 km, soit 10³ à 108 m) :
- 10³ m = 1 km :
- hauteur du mont Blanc : 4 808 m ;
- hauteur de l'Everest : 8 850 m.
- 104 m = 10 km :
- l'épaisseur de l'atmosphère terrestre est d'environ 90 km.
- 107 m = 10 000 km :
- diamètre de la Terre : environ 13 000 km ;
- circonférence de la Terre : environ 40 000 km.
Taille interplanétaire : (10³ à 108 m)
Ordre de grandeur des distances entre planètes dans le système solaire (de l'ordre de 100 000 à 10 milliards de km, soit 10³ à 108 m) :- 108 m = 100 000 km :
- distance parcourue par la lumière en une seconde : 300 000 km ;
- distance moyenne entre la Terre et la Lune : 384 000 km.
- 1011 m = 100 millions de km :
- distance moyenne entre la Terre et le Soleil : 150 millions de km, soit 1 ua.
- 1012 m = 1 milliard de km :
- demi-grand axe de l'orbite de Pluton : 5,9 milliards de km, soit 39,5 ua.
- 1013 m = 10 milliards de km :
- rayon du système solaire : 14,4 milliards de km, soit 93 ua.
Libellés : Infos et actualités, Messages aux classes de G.Marion, vocabulaire
29 novembre 2007
«Vive la science !»
 Oui, notre monde a de l'avenir ! A l'heure où planent dans les esprits de fortes inquiétudes qui ont pour nom réchauffement climatique, crise de l'énergie, nouveaux conflits nucléaires ou biologiques, terrorisme, épidémies planétaires... les plus grands scientifiques nous donnent de multiples raisons d'espérer Né juste après la Seconde Guerre mondiale, Sciences et Avenir a décidé de fêter ses 60 ans en leur posant les questions que vous, lecteurs, vous posez aussi aujourd'hui. Ils nous ont répondu avec sincérité et sérieux . Mais ils ont fait plus : ils nous ont avoué leurs rêves pour demain ! Quelle énergie ! Loin de succomber à une quelconque morosité, ils se montrent prêts à faire face à la complexité. Qu'elle émane de l'Univers tout entier, du cerveau humain, de l'ADN, du continent-microbes, ou encore des sociétés que l'homme bâtit... et détruit.
Oui, notre monde a de l'avenir ! A l'heure où planent dans les esprits de fortes inquiétudes qui ont pour nom réchauffement climatique, crise de l'énergie, nouveaux conflits nucléaires ou biologiques, terrorisme, épidémies planétaires... les plus grands scientifiques nous donnent de multiples raisons d'espérer Né juste après la Seconde Guerre mondiale, Sciences et Avenir a décidé de fêter ses 60 ans en leur posant les questions que vous, lecteurs, vous posez aussi aujourd'hui. Ils nous ont répondu avec sincérité et sérieux . Mais ils ont fait plus : ils nous ont avoué leurs rêves pour demain ! Quelle énergie ! Loin de succomber à une quelconque morosité, ils se montrent prêts à faire face à la complexité. Qu'elle émane de l'Univers tout entier, du cerveau humain, de l'ADN, du continent-microbes, ou encore des sociétés que l'homme bâtit... et détruit.Une dernière réflexion, sur l'échelle du temps. Si les politiques raisonnent à court ou moyen terme (élections obligent), les scientifiques, et c'est leur caractéristique, ne peuvent pas ne pas penser à long terme. Que l'un de ses génies (Newton, Einstein, Darwin...) découvre une nouvelle loi de la nature et c'est toute une façon de voir (piloter) le monde qui s'en trouve (pour toujours ?) modifiée. Qu'un groupe consensuel de scientifiques estime aujourd'hui que le climat va effectivement se modifier sous l'action de l'homme et c'est un nouvel avenir qui se dessine. S'il n'est pas pérennisé, le ponctuel «Grenelle de l'environnement» apparaîtra bien dérisoire... Mue par l'impérieux désir de comprendre puis d'expliquer, la pensée scientifique ne s'en arrêtera pas pour autant. Avec doute à la clé. Cette façon d'envisager le monde a tout l'avenir devant elle.

Sciences et Avenir
Libellés : Infos et actualités ; en librairie
28 novembre 2007
Professor and Chair
Les transformations de Möbius
L'ensemble des transformations de Möbius, est le sous-groupe des homéorphismes de
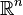 généré par les inversions, c'est-à-dire l'ensemble des composées d'un nombre fini d'inversions.
généré par les inversions, c'est-à-dire l'ensemble des composées d'un nombre fini d'inversions.Les principaux exemples de transformations de Möbius sont:
- Les translations (par composition de deux réflexions)
- Les isométries de
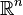 (par composition de n réflexions au plus)
(par composition de n réflexions au plus) - Les homothéties par composition de deux inversions par rapport à des sphères puis d'une isométrie)
Ce court film dépeint la beauté mathématique des transformations de Möbius. Les séquences du film tentent de montrer que le passage à une dimension supérieure peut rendre la compréhension plus facile .
Libellés : Images mathématiques, Récréation
Galileo Galilei (Galilée)
 La philosophie est écrite dans ce vaste livre qui constamment se tient ouvert devant nos yeux (je veux dire l’Univers), et on ne peut le comprendre si d’abord on n’apprend pas à connaître la langue et les caractères dans lesquels il est écrit. Or il est écrit en langue mathématique, et ses caractères sont les triangles, les cercles et autres figures géométriques, sans lesquels il est humainement impossible d’en comprendre un seul mot, sans lesquels on erre vraiment dans un labyrinthe obscur.
La philosophie est écrite dans ce vaste livre qui constamment se tient ouvert devant nos yeux (je veux dire l’Univers), et on ne peut le comprendre si d’abord on n’apprend pas à connaître la langue et les caractères dans lesquels il est écrit. Or il est écrit en langue mathématique, et ses caractères sont les triangles, les cercles et autres figures géométriques, sans lesquels il est humainement impossible d’en comprendre un seul mot, sans lesquels on erre vraiment dans un labyrinthe obscur.Galilée, l’Essayeur
Né à Pise en 1564, Galileo Galilei est le fils d’un musicien et compositeur florentin. D’abord novice au collège du monastère de Vallombrosa, il poursuit des études de médecine à l’université de Pise. Mais il est plus attiré par les mathématiques et quitte l’université sans diplôme. En 1588, sur la géographie de l’Enfer de Dante à l’Académie de Florence lui vaut les louanges de Guidobaldo del Monte qui l’aide à obtenir la chaire de mathématiques de Pise. A 35 ans, Galilée étudie les mouvements et décrit la chute des corps. Du haut de la tour de Pise, il lâche des balles de plomb, de bois, de papier et découvre que, quelle que soit leur masse, tous les corps sont animés du même mouvement. Il est également le premier à énoncer le principe de relativité. Lorsqu’on est à bord d’un navire qui vogue en ligne droite et à vitesse constante, on ne ressent aucun mouvement. On est immobile par rapport au navire mais le navire se meut par rapport à la Terre. En fait, rien n’est absolument immobile et tout dépend du référentiel dans lequel on se place.
En mai 1609, Galilée entreprend la construction d’une lunette afin de mener ses propres expériences. Cet instrument lui permettra aussi de gagner l’argent dont il manque cruellement. Il fabrique lui-même les lentilles et obtient une lunette grossissant six fois sans déformation de l’image. Fort de ce premier succès, il réalise une nouvelle lunette d’un grossissement de neuf. Il en fait la démonstration en août 1609 aux Sénateurs de la République de Venise. Ces derniers, enthousiasmés, y voient aussitôt des applications militaires. Mais le mérite de Galilée fut de braquer sa lunette, non pas vers la Terre, mais vers le ciel.
Partisan de Copernic depuis au moins vingt ans, Galilée enseigne pourtant à ses élèves de l’université la théorie de Ptolémée, couramment admise, selon laquelle la Terre se trouve au centre de neuf sphères concentriques portant les planètes et les étoiles. Il doit rester prudent face à l’Inquisition et à ses collègues, déjà peu enclins à la sympathie vis-à-vis d’un homme qui critique ouvertement l’enseignement d’Aristote.
Au début de l’année 1610, Galilée observe le ciel avec sa dernière lunette. En pointant l’instrument sur Jupiter, il découvre trois puis quatre étoiles alignées autour de la planète. Il trouve rapidement l’explication : Jupiter possède des satellites. En juillet de la même année, il devient « Premier mathématicien du studium de Pise et Premier mathématicien et Philosophe du grand-duc de Toscane » et s’installe à Florence en septembre ; ce contre l’avis de ses amis qui lui conseillent de rester à Venise, la seule puissance qui ose encore résister au Pape.
C’est à cette période que Galilée publie ses premiers résultats dans un ouvrage rédigé en latin : Le Messager des étoiles. Il y expose ses observations de la Lune, qui n’est pas une sphère parfaite mais se révèle montagneuse et accidentée. Il y donne également une explication de la "lumière cendrée" qui n’est autre que le clair de Terre reflété par la Lune. 1610 est une année faste pour Galilée. Il est au faîte de sa gloire et reçoit l’appui d’astronomes illustres comme Kepler ou encore Clavius, chef des astronomes du Pape. Il sera d’ailleurs invité à Rome l’année suivante et y rencontrera un franc succès. Dans le même temps, il poursuit ses recherches et fait de nouvelles découvertes qui se révèlent capitales. En pointant sa lunette sur Vénus, il observe des phases, comme celles de la Lune, et des variations de sa taille apparente. Pour lui, cela ne fait aucun doute : la planète tourne autour du Soleil et se déplace par rapport à la Terre.
Mais ces succès attisent les rancœurs et les ennemis de Galilée passent à l’offensive dès 1612, tant sur les plans scientifique que religieux. Les universitaires conservateurs, adeptes d’Aristote, condamnent les théories coperniciennes et s’acharnent contre l’un des disciples de Galilée, Castelli. Le vrai danger vient des théologiens, qui jugent le système copernicien contraire aux Ecritures. Galilée s’attache alors à prouver la compatibilité des Ecritures et du système héliocentrique. En 1616, il décide de se rendre à Rome afin de convaincre les ecclésiastiques du bien-fondé de ses théories. Il y rédige un opuscule sur les marées, preuves du mouvement de la Terre. Mais il est trop tard et en février 1616, les propositions coperniciennes selon lesquelles le soleil est le centre immobile du monde et la Terre se meut sont jugées hérétiques. En mars de la même année, l’ouvrage dans lequel Copernic expose ses théories est mis à l’Index et Galilée est prié de ne plus professer de telles hérésies. Il reste prudent pendant sept années et ne fait plus allusion aux théories coperniciennes.
En 1623, le cardinal Maffeo Barberini devient pape et prend le nom d’Urbain VIII. Jeune, sportif et libéral, il représente l’espoir des milieux intellectuels et progressistes. Galilée, qui connaît bien le nouveau pape, tente alors de réhabiliter Copernic. En 1624, il reçoit l’aval du pape pour la rédaction d’un ouvrage contradictoire sur les différents systèmes du monde, à condition qu’il soit parfaitement objectif. Galilée, malade, met plusieurs années à le rédiger et c’est en 1631 que le livre reçoit l’imprimatur sous réserve de quelques corrections. Dialogue où dans les rencontres de quatre journées il est disserté au sujet des deux principaux systèmes du monde, le ptoléméen et le copernicien, en proposant sans aucune détermination les raisons philosophiques et naturelles tant en faveur de l’une que de l’autre des parties sort des presses florentines en février 1632.
Coup de théâtre : le pape Urbain VIII, furieux, ordonne la saisie de l’ouvrage. Mais il est trop tard et il a déjà été diffusé. Galilée est convoqué au Saint-Office en septembre de la même année. Il ne s’y rend qu’en hiver, menacé d’arrestation. Comment expliquer la réaction du pape, pourtant libéral et ami de Galilée ? Il semble qu’Urbain VIII n’ait pas apprécié le fait que Galilée, malgré le titre de son ouvrage, n’ait pas respecté leur accord et qu’il se soit livré à l’éloge des théories coperniciennes. Mais Galilée apparaît également comme une victime de la raison d’état. En effet, Urbain VIII se trouve à cette époque dans une situation difficile. Il est soupçonné de favoriser les idées novatrices au détriment des valeurs traditionnelles et sa politique pro-française, alors que la France soutient les protestants, lui attire les foudres de nombres de catholiques. C’est donc pour calmer ses adversaires qu’il leur « offre » le procès de Galilée.
Les audiences débutent en avril 1632. Galilée est accusé d’avoir enfreint l’interdiction de 1616 de défendre les théories de Copernic. Il est jugé coupable en juin, doit abjurer ses erreurs et est assigné à résidence. Il s’installe alors dans sa maison de la banlieue de Florence et y séjourne jusqu’à sa mort le 8 janvier 1642. Galilée ne sera réhabilité qu’en 1757 avec le retrait de l’interdiction de 1616.
Source : Infosciences.frLibellés : Citations, Connaissance des mathématiciens, Histoire des mathématiques
27 novembre 2007
LE RÔLE DES MATHÉMATIQUES DANS L’ÉDUCATION:UN DOSSIER DU N° 119 DE LA REVUE TANGENTE , en kiosque le 28 novembre 2007
Tangente questionne le Ministre de l’Education Nationale et défend les thèmes qui lui sont chers : interdisciplinarité, décloisonnement des mathématiques et de la culture…
En octobre dernier, Monsieur Xavier Darcos a accepté de parrainer les manifestations liées aux 20 ans de Tangente, il a également répondu à une interview qui se voulait « engagée » et qui était l’occasion de mettre en avant une approche d’une pédagogie nouvelle défendue depuis longtemps par le magazine. Réponses in extenso p. 8… Le mythe de la toute puissance des maths, p. 12… Le Renaudot contre l’échec scolaire, p. 14… L’interdisciplinarité, axe prioritaire, p. 16…
Libellés : Infos et actualités ; en librairie
Algorithme
Suite finie de règles à appliquer,
- dans un ordre déterminé,
- à un nombre fini de données,
- en un nombre fini d’étapes
- pour arriver avec certitude, à un certain résultat et cela indépendamment des données.
Définition donnée par Wikipédia :
Un algorithme est un moyen pour un humain de présenter la résolution par calcul d’un problème à une autre personne physique (un autre humain) ou virtuelle (un calculateur). En effet, un algorithme est un énoncé dans un langage bien défini d’une suite d’opérations permettant de résoudre par calcul un problème. Si ces opérations s’exécutent en séquence, on parle d’algorithme séquentiel. Si les opérations s’exécutent sur plusieurs processeurs en parallèle, on parle d’algorithme parallèle. Si les tâches s’exécutent sur un réseau de processeurs on parle d’algorithme réparti ou distribué.
Les algorithmes dont on a retrouvé des descriptions exhaustives ont été utilisés dès l’époque des Babyloniens, pour des calculs concernant le commerce et les impôts.
L’algorithme le plus célèbre est celui qui se trouve dans le livre 7 des Éléments d’Euclide. Il permet de trouver le plus grand diviseur commun, ou PGCD, de deux nombres.
Soient deux entiers naturels a et b, dont on cherche le PGCD. Le cas où a ou b est nul ne nécessite aucun algorithme ; on l'exclut.
On commence par calculer le reste de la division de a par b, qu'on note r ; puis on remplace a par b, puis b par r, et on ré-applique le procédé depuis le début.
On obtient ainsi une suite, qui vaut 0 à un certain rang ; le PGCD cherché est le dernier reste non nul.
Calculons, par exemple, le pgcd de 1071 et 1029 (égal à 21) par cet algorithme avec les étapes suivantes :
| a | b | r |
| | ||
| 1071 | 1029 | 42 |
| 1029 | 42 | 21 |
| 42 | 21 | 0 |
Libellés : Histoire des mathématiques
26 novembre 2007
Une BD pour attirer les lycéens vers les premiers cycles universitaires scientifiques
 Le constat n’est pas nouveau, mais il n’en n’est pas moins regrettable : trop peu de bacheliers, et surtout trop peu de bachelières, s’orientent vers les premiers cycles scientifiques universitaires. La décroissance des effectifs est importante, notamment en physique et sciences de la nature et de la vie (respectivement - 47 et - 27 % en 5 ans). Les effectifs de la filière S étant globalement stabilisés depuis plus de 15 ans, ce sont les filières sélectives (IUT, écoles d’ingénieurs) et les études menant aux métiers de l’informatique ou aux sciences et techniques industrielles qui ont absorbé la quasi-totalité de cette déperdition. Or, il parait essentiel pour les universités, si elles veulent maintenir une activité de recherche innovante et performante, de disposer, dans leurs filières fondamentales, d’un vivier important d’étudiants issus de tous les horizons, auxquels elles peuvent offrir, sans doute plus qu’ailleurs, un enseignement favorisant le développement de leur curiosité, de leur esprit critique et de leur capacité à mener un projet de recherche. C’est donc pour mener une campagne d’information et de séduction, auprès des lycéens, de leurs parents et de leurs enseignants, que huit des universités franciliennes et le conseil régional se sont associés, en créant la bande dessinée
Le constat n’est pas nouveau, mais il n’en n’est pas moins regrettable : trop peu de bacheliers, et surtout trop peu de bachelières, s’orientent vers les premiers cycles scientifiques universitaires. La décroissance des effectifs est importante, notamment en physique et sciences de la nature et de la vie (respectivement - 47 et - 27 % en 5 ans). Les effectifs de la filière S étant globalement stabilisés depuis plus de 15 ans, ce sont les filières sélectives (IUT, écoles d’ingénieurs) et les études menant aux métiers de l’informatique ou aux sciences et techniques industrielles qui ont absorbé la quasi-totalité de cette déperdition. Or, il parait essentiel pour les universités, si elles veulent maintenir une activité de recherche innovante et performante, de disposer, dans leurs filières fondamentales, d’un vivier important d’étudiants issus de tous les horizons, auxquels elles peuvent offrir, sans doute plus qu’ailleurs, un enseignement favorisant le développement de leur curiosité, de leur esprit critique et de leur capacité à mener un projet de recherche. C’est donc pour mener une campagne d’information et de séduction, auprès des lycéens, de leurs parents et de leurs enseignants, que huit des universités franciliennes et le conseil régional se sont associés, en créant la bande dessinée" Objectif sciences : A la découverte des métiers scientifiques"
BDSciences.pdf
Libellés : Infos Bac S, Infos et actualités
MATH GIRL the superheroine of Calculopolis : Limite , quand x tend vers zéro, de sin(x)/x
Pour ceux qui préfèrent les maths à l'anglais
(ou l'anglais aux maths ) :
On peut travailler les deux ! et en même temps!
Libellés : Récréation
25 novembre 2007
Henri Lebesgue
Henri Lebesgue (1939)
Henri Léon Lebesgue ( né à Beauvais en 1875 - décédé à Paris en 1941) est un mathématicien français. Il est reconnu pour sa théorie d'intégration publiée initialement dans sa dissertation Intégrale, longueur, aire à l'Université de Nancy en 1902.
Henri Léon Lebesgue a révolutionné et généralisé le calcul intégral. Sa théorie de l'intégration (1902-1904) est extrêmement commode d'emploi, et répond aux besoins des physiciens. En effet, elle permet de rechercher et de prouver l'existence de primitives pour des fonctions « irrégulières » et recouvre différentes théories antérieures qui en sont des cas particuliers :
- fonctions en escalier et fonctions continues de Riemann
- fonctions bornées de Darboux
- fonctions à variation bornée de Stieltjes.
«
(Szolem Mandelbrojt)
Libellés : Citations, Connaissance des mathématiciens
Le Musée des Confluences

Le Musée des Confluences est en cours de construction à Lyon (Rhône), sous la maîtrise d'œuvre du département du Rhône.
Musée de sciences et de société, son propos est de confronter les savoirs scientifiques et le fonctionnement des sociétés.
Les trois grandes expositions de références traiteront des questions « D’où venons-nous ? », « Qui sommes-nous ? », « Que faisons-nous ? ». La première s'interrogera sur les origines et les fins qu’il s’agisse de la théorie du Big-Bang, de l’histoire de l’univers ou des différentes représentation de la mort dans les cultures du monde. La deuxième présentera l’homme au cœur de la biodiversité. Elle expliquera les mécanismes de l’évolution, la place de l’homme parmi les autres espèces animales, traitera de la spécificité de l’homme liée à son cerveau ou à sa propre représentation. La troisième enfin abordera le fonctionnement des sociétés : la coopération, la compétition, les processus créatifs, l’humanité en réseau ...
L'architecture du bâtiment que l'on pourrait rattacher au déconstructivisme est signée du cabinet autrichien Coop-Himmelb
Libellés : Art et mathématiques, Images mathématiques
24 novembre 2007
Vladimir I. Arnold
Vladimir I. Arnold
Vladimir Igorevitch Arnol'd, plus couramment appelé Vladimir Arnold est un mathématicien russe, né le 12 juin 1937 à Odessa, à l'époque en URSS.
Il a résolu le treizième problème de Hilbert avec Andreï Kolmogorov dans les années 1950.
Un de ses premiers résultats est le théorème de Kolmogorov-Arnold-Moser en dynamique. Il a reçu en 1982 le Prix Crafoord en même temps que Louis Nirenberg.
Il est membre de l'Académie des sciences de France (associé étranger) depuis le 16 avril 1984. Il travaille à l'Institut de mathématiques Steklov à Moscou et à l'Université Paris-Dauphine.
Libellés : Citations, Connaissance des mathématiciens
Chiffres en vrac .
15 916 employés (en septembre 2007)
1 200 employés millionnaires grâce aux stock-options dont 500 en dizaines de millions
13,1 milliards de dollars réserve de trésorerie
230 milliards de dollars de capitalisation boursière
La valeur de l'action a été multipliée par 8 en 3 ans
au moins 20 milliards de documents indexés
au moins 300 millions de requêtes par jour sur l'ensemble des sites
au moins 100 millions de vidéos visionnées chaque jour
environ 500 millions de visiteurs uniques mensuels sur l'ensemble des sites
1 million d'ordinateurs répartis dans plus de 60 data centers (fermes de serveurs)
850 téraoctets sont nécessaires pour stocker en cache toutes les pages indexées
835 millions de $ d'investissement en 2005
Une puissance de calcul de 600 teraflops : 10 fois plus que Columbia, l'ordinateur le plus puissant de la NASA
En mathématiques, le gogol est le nombre dont la représentation décimale s'écrit avec le chiffre un suivi de 100 zéros (10100).
La version anglaise de ce nom (« googol ») a été introduite en 1938 par le mathématicien américain Edward Kasner dans son livre Mathematics and the Imagination
C'est ce mot qui est à l'origine du nom de la société Google, ce nombre ayant marqué l'imagination des fondateurs :
« Google a choisi ce terme pour symboliser sa mission : organiser l'immense volume d'information disponible sur le Web »
Le gogol est approximativement égal à la factorielle de 70 (70!) et ses facteurs premiers sont seulement 2 et 5.
Il faut au minimum 334 bits pour représenter ce nombre.
En effet 2333 = 17498005798264095394980017816940970922825355447145699491406164851279623993595007385788105416184430592, mais il ne faut pas oublier le bit nécessaire pour représenter 20
Le gogol n'est pas utilisé scientifiquement, il sert surtout à l'enseignement des mathématiques. Kasner l'a créé afin d'illustrer la différence entre un nombre aussi grand et l'infini. En effet, bien qu'un gogol soit énorme, bien supérieur au nombre d'atomes dans l'Univers (1080 et des poussières), il est facile de l'écrire en notation conventionnelle, comme suit :
- 1 gogol = 10100
| 10 | 000 000 000 000 000 000 000 000 000 000 000 |
| 000 000 000 000 000 000 000 000 000 000 000 | |
| 000 000 000 000 000 000 000 000 000 000 000. 10gogol (un chiffre 1 suivi d'un gogol de zéros) est nommé un gogolplex |
Libellés : Infos et actualités
23 novembre 2007
Le chemin le plus court
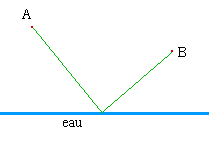
Quel est le trajet le plus court ?
Ne cliquez pas ici, c'est de la pub
Libellés : Enigme
Epreuve pratique de maths : dossier de L'APMEP
Descriptifs des sujets expérimentés en 2007
Rapport de l'inspection générale sur l'expérimentation de l'épreuve pratique au baccalauréat S
11/2007 : Discussion avec J. Moisan (IG) et M. Fréchet (APMEP) http://www.mathsdiscut.net/forum/
Libellés : Epreuve pratique
22 novembre 2007
Benoît MANDELBROT

L'anneau fractal de l'art à l'art à travers la géométrie, la finance et les sciences
Une conférence de Benoît MandelbrotBenoît Mandelbrot est un mathématicien franco-américain né à Varsovie le 20 novembre1924. Il a travaillé au début de sa carrière sur des applications originales de la théorie de l’information, puis développé ensuite une nouvelle classe d’objets mathématiques : les objets fractals, ou fractales.
Il signe en 1973 dans une revue d’économie un article au titre bien prudent : Formes nouvelles du hasard dans les sciences. Cet article répertorie les cas où, contrairement au paradigme classiquement utilisé, les aléas ne s’annulent pas, mais au contraire se cumulent, et où la prédiction statistique classique ne fonctionne plus. Il cite bien entendu des exemples pris dans son domaine à IBM, la transmission du signal, mais également dans des domaines inattendus : les crues du Nil, la forme des nuages, celle des fleuves.
Il arrive brillamment à la conclusion qu'il n'y a pas une forme de hasard, qui conduirait toujours à une égalisation par la loi des grands nombres. Il s’agit là d’une illusion due au fait que nous n’étudions que ces exemples en nous détournant des autres comme mal conditionnés, comme les mathématiciens se sont détournés de la courbe de von Koch qu’ils considéraient comme un objet monstrueux : les sphères ou les triangles sont considérés comme des objets acceptables par les mathématiciens de l’époque, mais pas les nuages ni les arbres (du moins en tant qu’objets géométriques). Les mathématiques de cette époque restent muettes sur les monstres. Pas étonnant dans ces conditions que les mathématiques existantes soient considérées comme ayant un immense pouvoir d’explication des phénomènes scientifiques, car nous ne considérons comme scientifiques que les phénomènes qu’elles permettent d’expliquer ! Nous sommes pris dans le piège d’un argument circulaire dont nous ne pouvons plus sortir.
Or, ajoute Mandelbrot, c’est l’essentiel des phénomènes de la nature qui obéissent à cet autre type de hasard où l’on ne peut appliquer la loi des grands nombres. Le modèle standard nous fait passer à côté de la plus grande partie de la réalité, et va jusqu’à nous empêcher même de la voir.
Il cite alors comme exemple de cette nouvelle forme de hasard à étudier l’exemple qui deviendra célèbre de la côte de Bretagne, dont la longueur dépend de l’échelle à laquelle on la mesure, et qui possède une dimension de Hausdorff non-entière, comprise entre 1 et 2 : elle ne constitue à proprement parler ni un objet à une dimension, ni un objet à deux dimensions, et c’est en acceptant l’idée de dimension non-entière que nous allons pouvoir attaquer ces objets qui ont toujours échappé à notre étude : la théorie fractale est dès cet article officieusement lancée.
Libellés : Art et mathématiques, Conférence, Connaissance des mathématiciens
21 novembre 2007
Garrett Lisi : simple Brice de Nice ou Einstein moderne ?
L’homme n’est pas banal. A 39 ans et diplômé en physique théorique depuis 1999, il n’est membre d’aucune université et partage son temps entre le surf, le snow board et autres sports de glisse, et la recherche solitaire des lois ultimes de la physique. On pourrait facilement ne pas le prendre au sérieux. Mais inévitablement, quand un physicien de la carrure d’un Lee Smolin déclare à propos de la théorie de Garrett Lisi que « c’est l’un des modèles d’unification les plus convaincants que j’ai vu depuis de longues années », le côté un peu hippie et même New age de cette histoire lui confère illico une belle réussite médiatique...
Par Laurent Sacco, Futura-Sciences
La suite est ici
Libellés : Infos et actualités
Calcul mental: deux cas parmi d'autres
Concours WIMS
Pour la 5ème année consécutive, le concours wims a lieu juste avant les congés de Noël. Il permet aux professeurs de mathématiques de proposer aux élèves une animation mettant en oeuvre l’informatique et les mathématiques. Chaque participant reçoit un cadeau. Pour consulter la liste complète des lots :
Libellés : Infos et actualités, Messages aux classes de G.Marion
20 novembre 2007
Le groupe de Lie E8 , dont le nom est bien connu des mathématiciens,fonderait une "théorie du tout" qui jette le trouble chez les physiciens
Albert Einstein a légué à ses pairs une question toujours ouverte, peut-être la plus profonde jamais posée par la physique : toutes les lois de l'Univers peuvent-elles être décrites par une seule et même théorie ?
Vouloir y répondre, c'est faire montre d'une prétention inouïe. Mardi 6 novembre, Garrett Lisi poste sur le serveur d'archives de l'université Cornell (ArXiv. org), un article de 31 pages au titre fleurant le canular :
"Une théorie du tout exceptionnellement simple".
Ce que propose le physicien est une "théorie de grande unification" – selon l'expression consacrée –, c'est-à-dire capable de réconcilier les deux grandes branches de la physique léguées par les travaux d'Einstein.
Pour ce faire, explique Carlo Revelli, du Centre de physique théorique de Marseille, « nous sommes confrontés à deux problèmes . Le premier consiste à décrire avec les mêmes équations les quatre forces fondamentales de la nature : l'interaction forte, l'interaction faible, la force électromagnétique et la force gravitationnelle », explique le chercheur. « Le second consiste à rendre compatibles les deux théories que sont la mécanique quantique et la relativité générale." »
Toute la théorie de Garrett Lisi repose sur un objet mathématique complexe, le "groupe de Lie exceptionnel" E8, ici utilisé pour décrire les interactions fondamentales et les particules élémentaires qui composent l'Univers.
Interaction forte : force responsable de la cohésion des noyaux atomiques.
Interaction faible :force responsable de l'émission de particules par certains atomes, c'est-à-dire de la radioactivité.
Mécanique quantique : ensemble des lois qui régissent les mouvements et les interactions des particules élémentaires et des atomes. Elle ne s'applique pas au monde macroscopique.
Relativité générale : théorie formulée par Albert Einstein pour décrire l'influence des objets massifs sur la structure de l'espace-temps. Elle ne s'applique pas au monde de l'infiniment petit.
Source: Le Monde.fr l'article complet est ici
Libellés : Infos et actualités
Il y a près de 4 siècles ,Descartes expliquait comment construire le produit de deux nombres, pour "le fun", bagatelle destinée à étayer sa "méthode"
Le principal apport de Descartes en mathématique est l'application des méthodes de l'algèbre aux problèmes de la géométrie, pratiqués presque sans changement depuis l'antiquité . Mais les mathématiques ne sont pour lui qu'un moyen d'éprouver sa méthode, de s'y exercer, car il n'y a pas de science à laquelle on puisse demander des exemples aussi certains et évidents ;
mais il n'en ferait pas grand cas si elle ne servait…
« qu'à résoudre les vains problèmes dont les calculateurs et les géomètres ont coutume d'amuser leurs loisirs ; et je croirais, dans ce cas, n'avoir réussi qu'à m'occuper de bagatelles avec plus de subtilité peut-être que les autres. »
cliquer sur l'image pour l'agrandir
Libellés : Connaissance des mathématiciens, Histoire des mathématiques
19 novembre 2007
Logique Shadok
Un beau soir de 1968, le 29 avril exactement, entre le journal de 20 heures et le grand film, apparurent de drôles de bipèdes, débiles et hauts sur pattes, dont la principale préoccupation était de fuir une planète multiforme, en inventant un tas de trucs qui ne marchaient jamais....
Les Shadoks, sortes d'oiseaux rondouillards avec de longues pattes et de petites ailes ridicules ont été ainsi baptisés pour la consonance anglo-saxonne du nom et en clin d'œil au capitaine Haddock, selon leur dessinateur.
Ils ont pour ennemis les Gibis, coiffés d'un chapeau melon leur permettant de réfléchir tous ensemble aux problèmes en se moquant des inventions des shadoks - et qui doivent leur nom à « la prononciation anglaise des initiales de la Grande-Bretagne ».
Les Shadoks possèdent pour tout vocabulaire quatre mots monosyllabiques : « ga, bu, zo, meu ». Les Shadoks sont excessivement méchants, et idiots par définition. Ils réalisent des machines improbables qui ne fonctionnent pas; l'inventeur étant, presque systématiquement, le Professeur Shadoko : la liste est longue ! La cosmopompe, destinée à pomper le cosmogol 999 aux Gibis (série BU) ; la machine à pilules, qui faillit coûter la vie aux derniers rescapés shadoks (série ZO) ; etc...
L'extrait présenté ci-dessous est un cours de logique Shadok
Libellés : Récréation
18 novembre 2007
Des mathématiques pour détecter les tumeurs à la manière des chauves-souris
Des scientifiques écossais tentent de mettre au point un radar imitant celui des chauves-souris afin de détecter les tumeurs à l’intérieur du corps humain.
L’équipe de chercheurs du Dr Hayward travaille en collaboration avec des mathématiciens afin de mettre au point de tels codes acoustiques qui permettront d’identifier plusieurs cibles, incluant des cellules cancéreuses.
Source: BBC
Libellés : Infos et actualités
Calcul formel :Pourquoi et comment utiliser XCAS au lycée ?(par Guillaume Connan)
XCAS existe depuis quelques années mais est très mal connu au lycée car sa puissance fait peur. XCAS permet en effet de traiter des problèmes très sophistiqués, mais, ce qu'on passe souvent sous silence, des problèmes très simples qui permettent par exemple d'initier des élèves de l'école primaire à la programmation !
Nous commencerons en abordant la géométrie dynamique au lycée car c'est un domaine où une comparaison avec les logiciels massivement utilisés par les professeurs du secondaire est possible, ce qui n'est pas le cas du calcul formel, de la programmation et surtout la possibilité d'associer les trois plus le tableur qui constitue une des grandes forces de XCAS.
Nous poursuivrons par un sujet de l'épreuve pratique de Terminale S qui défraie la chronique actuellement et effraie nombre de collègues.
Nous traiterons ensuite un problème que ni un logiciel de géométrie classique, ni un tableur ne peuvent traiter et qui est pourtant très intéressant mathématiquement.
Nous finirons par un exemple de TP donné en Terminale S et qui utilise un soupçon d'algorithmique.
Guillaume Connan 2007-11-13
Libellés : Epreuve pratique, Infos et actualités
Massachusetts Institute of Technology
( Institut de Technologie du Massachusetts) est une institution de recherche et une université américaine, spécialisée dans les domaines de la science et de la technologie.
Située à Cambridge, dans le Massachusetts, à proximité immédiate de Boston, elle est considérée au XXIe siècle comme la meilleure université occidentale en sciences et en technologies.
" Au départ, Benjamin et Romain étaient juste venus passer au MIT la dernière année de leur école d’ingénieur, les Ponts (après Polytechnique) pour l’un, Centrale pour l’autre. Mais, très vite repérés par leurs professeurs pour leur bon niveau, ils ont été poussés à faire un doctorat. Pour le financement de ces deux ou trois années d’études supplémentaires, pas de souci. Le labo qui les accueille – le Center for Energy and Environmental Policy Research pour Romain et l’Institute for Soldier Nanotechnologies (ISN), pour Sylvain – finance les frais d’inscription (de l’ordre de 40 000 dollars) et leur verse entre 1 500 et 2000 dollars net de salaire par mois. Même chose pour Benjamin, sorti de Supelec, lui, qui a été happé par le Humans and Automation Laboratory, «Hal», clin d’œil à l’ordinateur de 2001, l’odyssée de l’espace. Laure-Anne, elle, a quitté la France après le bac pour rejoindre Wellesley College, sans vraiment savoir ce qu’elle ferait. Trois ans plus tard, elle prépare un PHD de bio-ingénierie, tous frais financés par son labo. «Ici, les études sont très pratiques. On travaille pour sa recherche, avec des objectifs précis», explique Laure-Anne. Cela commence même avant le Master. Les undergraduates en sciences rejoignent une équipe de recherche dès leur première année universitaire...
Cette capacité à mélanger les disciplines n’est pas plus facile à obtenir à Boston qu’ailleurs, mais au moins, ici, tout est fait pour la faciliter. Ceux qui font tomber les cloisons pour innover sont plébiscités. C’est ainsi qu’est né le Media Lab, créé par Nicholas Negroponte. Installé dans un immeuble de Pei, ce labo qui «invente le futur» met la technologie au service de la vie courante : peluches communicantes pour aider les enfants malades, prothèses intelligentes pour réparer les handicaps, voitures électriques en libre service pour rendre les villes plus pratiques, ordinateur à 100 dollars… Les projets les plus fous naissent ici. Et les moyens suivent, apportés par les nombreux partenariats avec les entreprises. Moyens et interdisciplinarité, de quoi attirer des chercheurs pourtant heureux à Paris ! Tod Machover a longtemps été le directeur de la recherche musicale de l’Ircam, près du Centre Pompidou, mais il est venu créer le département informatique et musique du Media Lab, où l’on invente de nouvelles techniques d’apprentissage de la musique et de composition.
Des chercheurs sous pression
Quant à Federico Casalegno, ce chercheur qui réinvente depuis Boston les lignes de bus de la RATP avec des abris multimédias, il arrive tout droit de la Sorbonne où il réfléchissait aux nouveaux réseaux sociaux créés par Internet et le portable, dans un labo financé par Philips Design.
Cette interdisciplinarité, tous la recherchent. Elle permet par exemple à Fredo Durand, spécialiste de la synthèse d’images en 3D et de la simulation de la lumière, du Computer Science and articifial Intelligence Laboratory (Csail) installé dans le Stata Center, de mieux comprendre la perception des images par le cerveau en travaillant avec un confrère spécialisé en neurologie du Broad Institute (un laboratoire de recherche en génétique et neurosciences créé grâce à un don de 100 millions de dollars du fondateur du groupe immobilier Kaufman & Broad). Ces rencontres sont importantes pour des chercheurs toujours sous pression. Au MIT comme à Harvard, un scientifique ne doit pas seulement chercher, mais aussi trouver. Sinon, il a du mal à trouver des fonds pour poursuivre sa recherche, qu’ils soient d’origine publique (c’est le cas de 80 % des allocations de recherche du MIT) ou privée. L’autre règle, c’est celle du publish or perish : «publier ou périr», littéralement. On ne peut pas rester indéfiniment maître de conférences dans une université. Au bout de six ou sept ans, soit elle vous titularise professeur, soit on la quitte. Et la titularisation dépend du nombre et de la qualité des articles de recherche publiés dans les revues spécialisées. Malgré cette pression, Fredo Durand continue à préférer le système américain.
Pas seulement à cause de son salaire de 130 000 dollars. Pour lui, la séparation grandes écoles-université est trop néfaste : on sépare les meilleurs étudiants de chercheurs, sans perméabilité.
Chercheur très reconnu dans sa discipline, courtisé par les entreprises comme Adobe, il a toutes les chances d’être titularisé cette année et ne voit aucune raison de revenir.
Anne Lemiere n’a pas la même vision. Cette pression permanente de la publication – qui oblige parfois à écarter une recherche qui ne donnerait pas de résultats rapides – la gêne. Non sans hésitation, cette brillante astrophysicienne, formée à Paris-VI-Jussieu, va rejoindre l’Institut de physique nucléaire d’Orsay sur un poste du CNRS. «Le CNRS offre une grande liberté aux chercheurs. C’est unique et ça attire aussi les étrangers», assure-t-elle."
Source : Le Figaro.fr ; l'article complet est ici
Libellés : Infos et actualités
17 novembre 2007
Zero: La biographie d'une idée dangereuse . (Charles Seife)
 Une passionnante histoire de zéro....De rien... Du vide...
Une passionnante histoire de zéro....De rien... Du vide... Libellés : Infos et actualités ; en librairie
16 novembre 2007
Image mathématique : Art abstrait géométrique

Victor Vasarely, (1908-1997) est un artiste souvent reconnu comme le père de l'Op art.
l'Op art, art cinétique, ou "optique", est un terme utilisé pour décrire certaines peintures faites à partir des années 1960 et qui exploitent la faillibilité de l'œil à travers des illusions optiques.
Vasarely développa son propre modèle d'art abstrait géométrique, employant un nombre minimal de formes et de couleurs. Son travail lui a valu une renommée internationale et il a reçu plusieurs prix prestigieux.
Libellés : Art et mathématiques, Images mathématiques
Kurt Gödel et la folie de la logique.

Les Démons de Gödel. Logique et folie, par Pierre Cassou-Noguès. Éditions du Seuil, 2007, 284 pages, 21 euros.
Jusqu’où la créativité du célèbre mathématicien doit-elle être associée à sa paranoïa ? interroge le dernier livre de Pierre Cassou-Noguès.
Qu’il y ait eu des savants, et parmi les plus illustres, qui furent, par ailleurs, en proie au délire, pourquoi ne pas songer à l’intérêt que Newton marqua pour l’alchimie, voire l’astrologie, dans des papiers depuis retrouvés ? Sans, même, penser à de grands mathématiciens tels Cantor ou Turing (théoricien de la calculabilité). Mais, justement, peut-on forclore le « sujet » humain dans les disciplines formelles ? Ou bien ledit « sujet » réapparaît-il ou, plutôt, ne disparaît-il jamais dans ses œuvres les plus rationnelles ? Et, surtout, de quel « sujet » s’agit-il ? Le livre, passionnant, informé et de lecture aisée de Pierre Cassou-Noguès nous présente une intéressante étude de cas qui ne prétend pas trancher définitivement toutes ces questions. Cassou-Noguès a dépouillé les archives Gödel à l’université de Princeton et a fait son miel de la transcription, encore partielle et incomplète, des notes de Gödel rédigées avec une sorte de code sténographique. Par ailleurs, agrégé de mathématiques, il connaît les travaux scientifiques de Gödel ainsi que le « contexte » qui leur donne tout leur sens. Allons au plus court : Gödel, surtout vers la fin de sa vie, fait montre de traits paranoïaques assez typiques : peur d’être empoisonné (il est quasiment mort d’inanition), d’être la proie de fantômes, peur panique d’être assiégé par un « autre ». On laissera l’interprétation des symptômes à la science des analystes et des psychiatres (il a, un temps, fréquenté un jungien, dont il fut même le patient).Par ailleurs, c’est plus intéressant, mais nous ne sommes pas encore au cœur du débat, Gödel ne croit pouvoir rendre compte des idéalités mathématiques qu’en les séparant du « monde sensible », comme si, pour vraiment pratiquer les mathématiques, il faudrait ne plus avoir de corps, - être un ange, pourquoi pas ? Gödel en vient presque à reprendre la fin du Phédon : c’est l’esprit qui a tout organisé. « Platonisme », dira-t-on, mais en un sens très vague et très banal. Ou Platon relu par Leibniz (p.219). Ce qui est plus difficile à saisir et expliciter, c’est la position d’un sujet qui élabore un savoir établissant que si n’est pas exclue « la possibilité d’une démonstration métamathématique de la consistance de l’arithmétique », ce qui est, en revanche, exclu, « c’est la possibilité de refléter cette démonstration dans les déductions formelles de l’arithmétique » (Le théorème de Gödel, Seuil, 1997, p.91). Position d’un sujet : on ne confondra pas le sujet qui trouve une démonstration (et, en ce domaine, il n’y a pas de recette, rien n’est automatisable) et la démonstration elle-même que l’on peut, ensuite, exposer sans référence au processus grâce auquel elle a été élaborée. La découverte de Gödel sera plus compréhensible lorsque, quelques années après la publication de son travail (1931), Turing donnera une définition précise de la notion de système formel (1936-7) : s’il apparaît qu’ « une machine de Turing ne peut pas prouver la consistance du système dans lequel elle travaille ou ne peut pas écrire une formule qui exprime la consistance des règles qui déterminent son fonctionnement (si celles-ci sont bien consistantes) » (Cassou-Noguès, p.121), le théorème de Gödel nous renseigne-t-il, d’abord et avant tout, sur les limites de l’axiomatisation, d’une partie de l’arithmétique puis, plus généralement, de tout système formel axiomatisé ? Les axiomes de l’arithmétique sont essentiellement incomplets, toutes les vérités arithmétiques ne peuvent donc être obtenues en les déduisant formellement à partir des axiomes de l’arithmétique. Ou bien le sujet se trouve-t-il, également, mis en jeu ? Comme si - la comparaison est osée, mais elle n’est pas déplacée - la distinction, conceptuellement très claire, entre mathématique et métamathématique, trouvait son homologue dans une sorte de scission, interne au sujet, entre un sujet mathématicien et un sujet métamathématicien. Ce qui pourrait conduire, dans une économie psychique singulière, quasiment à une dissociation, le sujet métamathématicien devenant l’autre du sujet mathématicien (p.109). Voire le Grand Autre, le Tout Autre : Dieu et/ou le diable (hypothèse prudemment émise, pp. 160 sq, les textes de Gödel ne sont ni très nombreux ni très clairs, mais ils ne sont pas tous encore déchiffrés). Et l’expérience, assurément réelle, de l’intuition à l’œuvre dans les découvertes mathématiques, mènerait, elle aussi, à une scission du sujet, - telle une productivité de ce dernier qui, en quelque sorte, lui échappe : un peu comme l’autre scène, l’inconscient freudien (pp.86 sq.). Ce n’est qu’une piste : à cet instant, il deviendrait possible de commencer d’établir des liens entre la pratique de chercheur en mathématiques de Gödel et la configuration singulière de son économie psychique. Ce vers quoi pourrait nous conduire Cassou-Noguès. Affaire à suivre.
(*) Un ensemble donné de postulats servant de fondement à un système est « consistant » lorsqu’il est exclu qu’on puisse en déduire des théorèmes contradictoires, soit les propositions p et non-p.
Jean-Pierre Cotten, philosophe
Libellés : Infos et actualités ; en librairie
15 novembre 2007
Epreuve pratique et "mathématiques sexy".
Intervention d’un participant :
Ce que j'ai voulu dire en parlant de rendre les mathématiques "sexy", c'est qu'il faut montrer à travers des programmes et des pratiques rénovés que nous enseignons des mathématiques d'aujourd'hui, de notre temps celles qui sont présentes dans tous les appareils et artefacts quotidiens (téléphone portable, internet, jeu vidéo, TNT, etc.) avec les méthodes d'aujourd'hui. Ce n'est pas du lobbying. C'est un désir de redonner à notre discipline le lustre qu'elle a perdu.
Je crois qu'on peut donner une formation d'aussi bonne qualité tant en contenus qu'en compétences acquises en enseignant les mathématiques discrètes, les statistiques ou l'algorithmique qu'en enseignant la géométrie d'Euclide !
Je pense aussi que l'outil informatique est devenu indispensable à un enseignement moderne et efficace des mathématiques. C'est dans ce sens que je souhaite avancer. »
Libellés : Epreuve pratique
Cent cinquante courbes mathématiques.
Lien déniché par Le Math'Ador , l'excellent blog d'Olivier Legay
Libellés : Courbes ou surfaces mathématiques, Infos et actualités
14 novembre 2007
Histoire et enseignement des mathématiques
Le 21 novembre 2007 ,dans le cadre des mercredis de l'INRP , Evelyne Barbin et Anne Boyé communiqueront les résultats de leurs travaux.
Autour de l’ouvrage Histoire et enseignement des mathématiques : rigueurs, erreurs et raisonnements, INRP, 2007
Quels sont les apports de l’histoire des mathématiques pour la réflexion sur l’enseignement mathématique et scientifique aujourd’hui ? Dans la formation des enseignants et dans la classe ? Quatre équipes de professeurs de mathématiques ont travaillé sur ces questions dans le cadre d’un projet IREM-INRP. Leurs travaux montrent que les idées de rigueur, d’évidence et de démonstration ont changé au cours des époques.
Ces constats suscitent de nombreuses questions sur les apprentissages. Qu’accepte-t-on comme rigoureux, comme évident ? Que décide-t-on de démontrer ? Quand et pourquoi ? Est-ce qu’il y a des niveaux de rigueur et d’abstraction au cours de la scolarité ? Quelles explicitations, quelles réponses, les enseignants doivent-ils élaborer pour eux-mêmes ou pour leurs élèves ?
Intervenantes
Evelyne Barbin, professeur des universités en histoire des sciences, université de Nantes, responsable de la commission inter-IREM « épistémologie et histoire des mathématiques »
Anne Boyé, professeur agrégé de mathématiques associé à l'INRP, animatrice à l'IREM des Pays-de-la-Loire
Site EducMath
VOUS INSCRIRELibellés : Histoire des mathématiques, Infos et actualités
L'homme qui calculait
 Sujet : Bagdad au XIIIème siècle : Beremiz, un jeune berger, avait tellement l'habitude de compter ses moutons, puis de dénombrer, d'un seul coup d'oeil, les feuilles d'un arbre, les cailloux, les troupeaux, qu'il devint un grand "calculateur ". Par hasard, il fit la connaissance de Salim qui, très impressionné par sa facilité à résoudre les problèmes les plus difficiles, le présenta au vizir, puis au cheikh Lezid. Celui-ci va le nommer précepteur de sa fille. Mais, dans le contexte de la vie musulmane, il n'aura pas le droit de la rencontrer pour lui donner des cours de maths. Il le fera donc caché par un rideau... Sera-t-elle aussi impressionnée que les autres par l'intelligence redoutable de ce berger ? et par l'intelligence seulement ?...
Sujet : Bagdad au XIIIème siècle : Beremiz, un jeune berger, avait tellement l'habitude de compter ses moutons, puis de dénombrer, d'un seul coup d'oeil, les feuilles d'un arbre, les cailloux, les troupeaux, qu'il devint un grand "calculateur ". Par hasard, il fit la connaissance de Salim qui, très impressionné par sa facilité à résoudre les problèmes les plus difficiles, le présenta au vizir, puis au cheikh Lezid. Celui-ci va le nommer précepteur de sa fille. Mais, dans le contexte de la vie musulmane, il n'aura pas le droit de la rencontrer pour lui donner des cours de maths. Il le fera donc caché par un rideau... Sera-t-elle aussi impressionnée que les autres par l'intelligence redoutable de ce berger ? et par l'intelligence seulement ?...Commentaire : La réédition d'un grand classique. Ce n'est pas seulement la fille du cheikh qui est invitée à se perfectionner en arithmétique, mais le lecteur lui-même qui se piquera au jeu de résoudre les énigmes et de comprendre les leçons de calcul. Extraordinaire pour donner le goût des mathématiques ! Par ailleurs la trame du récit de rapproche davantage des Contes des Mille et Une Nuits... savante alchimie. Les prières incessantes à Allah, quant à elles, permettront de mieux se familiariser avec l'Islam et avec cette époque du moyen âge. Une grande paix émane de ce livre, qui pourtant présente la matière qui rebute souvent le plus en classe
Libellés : Infos et actualités ; en librairie









